

Model.AddGoal(null, GoalKind.Minimize, Model.Sum(x)) Model.AddConstraint(null, constraints = Model.GreaterEqual(Ax, b))
Ms excel solver function code#
For your problem, this is of course not an issue.įor completeness, to formulate the LP problem instead, exchange the code between START NLP SECTION and END NLP SECTION with the following code: var m = A.GetLength(0) įor (var i = 0 i < n ++i) Ax += A * x If I am not mistaken, unlike GRG, Solver Foundation cannot support general non-linear constraints out-of-the-box, I believe you will need additional plug-ins to handle these. Generates the following solution, which should be in line with the solution from the linked Excel sheet: f = 254184688.179922 Here is my code for Solver SDK: static double A = new double ", i, x.GetDouble()) One of the limits of the Excel Solver is that it will only give one root even though we know there is a second one.
Ms excel solver function how to#
However I can't seem to get anywhere with them because with MSF I can't figure out how to define the goal and with Solver SDK I always get back status "optimal" and a solution of all 0s which is definitely not even a local minimum. By clicking on Solve, Excel will execute the operation you asked it to and will give you the solution x 0,85078105. I have tried to replicate this in C# using either Microsoft Solver Foundation or Solver SDK.

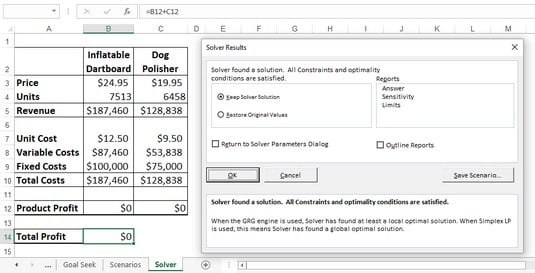
For information about how to do that, see Using the Solver VBA Functions. Before you can use this function, you must have the Solver add-in enabled and installed. Note The Solver add-in is not enabled by default. So instead of using standard linear algebra I use Solver with the non-negative constraint, minimizing the sum of the squared differences, and get a reasonable solution. Equivalent to clicking Solve in the Solver Parameters dialog box. I am solving the classic A x = b problem but with the caveat that all components of x must be non-negative. My problem is shown in the following spreadsheet. It can be solved in Microsoft Excel with the Solver add-in, but I am having trouble replicating that in C#. I have a non-linear optimization problem with constraints.


 0 kommentar(er)
0 kommentar(er)
